So, what if the Earth is round?

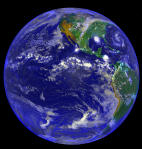
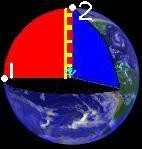
How do we know where we are on the Earth? The Earth is round and so far we have only dealt with maps representing two dimensions. Take a look at the picture of the earth.  We can identify it as being a part of a sphere, we can notice that it has a top and bottom, a side that you can see and a side that you cannot see.  How can we clearly identify every point on this spherical surface? In the picture to the left, we can see a ladder running down the center of the sphere, from the top to the bottom along the axis of rotation of the earth, with a stick figure on on it at a point exactly half way between the top and the bottom, looking perpendicular (at a right angle) to the ladder, towards point one, on the surface of the earth, to the stick figure's left.  We will call this point the origin, the exact place that all other points will be defined in relation to in our coordinate system, the method by which we will define all points on the globe.  If the ladder was to spin around in a circle, a full 360 degrees of rotation, without the stick figure changing the angle between its eyes and the ladder, all of the points traced out by the stick figure's eyes form a circle that we will call the equator.  If we were to cut the globe along the equator, we would be left with two identical half spheres, save for orientation (round side or flat side pointing up). We will call the top half of the sphere the Northern Hemisphere and the bottom half of the sphere the Southern Hemisphere. Now that the ladder has completed its rotation of 360 degrees, the stick figure will be once again, looking at the origin.  If it was to want to see the top of the sphere, at point two, it would have to tilt its head back 90 degrees, with its head looking directly up the ladder.  Similarly, if it wanted to see the bottom of the globe, that would require tilting its head 90 degrees down, until looking along the axis of the ladder.  The semicircle that the stick figure traces out between the north and south poles that crosses the origin is called the prime meridian. Now, let's place a compass rose at the original point at which the stick figure was looking, at the origin, on the surface of the sphere.  North points towards the Northern Hemisphere, South, towards the Southern Hemisphere, East towards the right, and west points towards the left.  Now, we will define the location of the origin as being at 0 degrees north, 0 degrees west (or, similarly, 0 deg. South, 0 deg. East).  If we were to want to look at the extreme top of the sphere, without rotating at all, we would tilt our heads ninety degrees North.  Therefore, the location of the Northernmost point on the globe is 90 N. To see the extreme bottom of the sphere, we would tilt our heads ninety degrees South, so the Southernmost point on the globe is located at 90 S.  Looking at the origin once again, in order to see the point directly behind us, we could either rotate 180 degrees East or 180 degrees West.  So the point directly behind us could be addressed by 0 North, 180 West, or 0 South, 180 West, or 0 North 180 East.  There are many ways that we can define each point, each just as good as the next!  Standard convention has longitude as being measured to the West, with a negative sign sometimes used to denote movement East.  Latitude generally appears in degrees North or South.  We will soon see why it is crucial to keep our signs organized. But first, here's a good way to remember the names latitude and longitude with their corresponding lines on a globe.  On a globe, lines of latitude and longitude are generally marked ten or five degrees apart, respectively.  If our stick figure, still on the spinning ladder in the middle of globe wanted to see a point at a latitude other than 0 degrees, without rotating his head, he would have to climb up or down on the ladder and then spin to the correct longitude.  So when the stick figure changes its position on the ladder, it can trace out a new line of latitude.  If we look at the length of the lines of latitude and longitude, we can see that the lines of longitude always wrap all of the way around the earth through the North and South poles, each having the circumference of the earth.  Lines of latitude, on the other hand, are circles that vary in radius between that of the earth, at the equator, and zero, at the poles.  So remember, lines of longitude are always long.

Now that we can describe where exactly any point on the surface of a sphere is, let's investigate how we can determine the distance between any two points on a sphere. If we are given any two points on a sphere, we can connect them with an arc, a part of a circle. We will call the circle containing this arc a Great circle. There exists a Great circle for every set of points on a sphere and each has the same circumference, that of the sphere. We know that the circumference of a circle is equal to (2r)pi. Since an arc is part of a circle, the length of an arc is equal to the a ratio corresponding to how much of a circle the arc completes, which is equal to the number of degrees of the arc divided by the number of degrees in a circle, multiplied by the circumference of a circle of that radius. 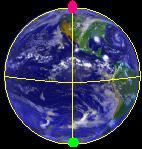Length of an arc with n degrees and radius r = (2r)pi * (# degrees in the arc/360) Let's say that we want to determine the distance along the Earth's surface between the North Pole (90 N, gray dot) and the South Pole (90 S, green dot).  How far must we travel? Click Here for the Solution Click Here for Detailed Hints That wasn't too difficult, was it?  Now we can see that any two points are connected by a great sphere, and that determining the distance between the two points is a matter of figuring out how many degrees along that great circle there are between those two points.  This wasn't too hard when the two points only differed in displacement in one direction - in the example above, the longitudes were the same.  But how do we determine the number of degrees that separate the points in the great circle when they differ in location by both latitude and longitude, in other words, when the great circle is parallel to neither the equator nor the prime meridian? Determine the distance between Tananarive, Madagascar located at 18 S 47 E, and New York City, New York, USA, located at 40 N 73 W. Click Here for the Solution Click Here for Detailed Hints

1. Coordinate System
2. Origin
3. Scale Length